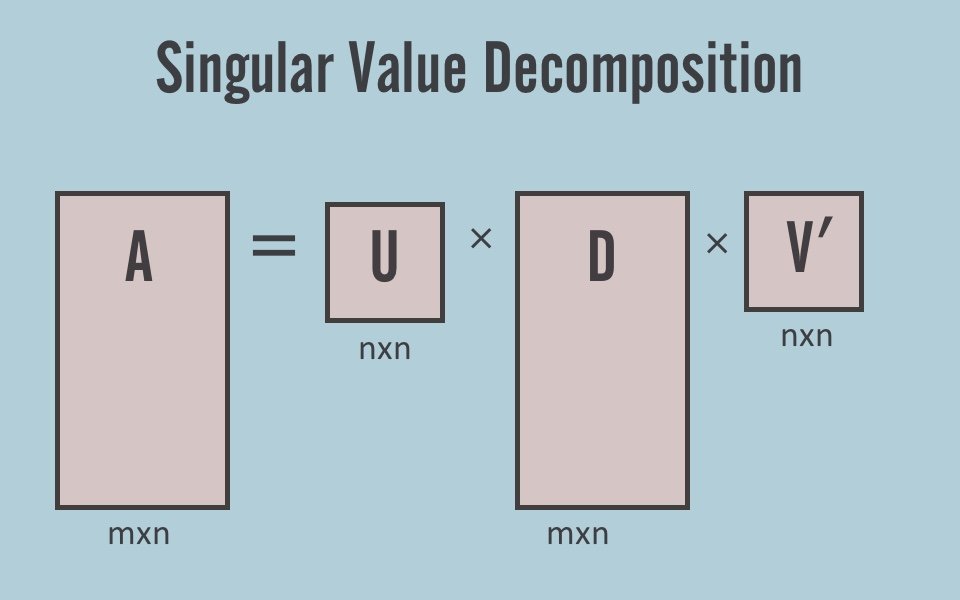
SVD (Singular Value Decomposition) is a factorization of a real or complex matrix. It is the generalization of the Eigen-Decomposition of a positive semidefinite normal matrix (for example, a symmetric matrix with positive eigenvalues) to any matrix.The singular value decomposition of a matrix A is the factorization of A into the product of three matrices A = UDVT where the columns of U and V are orthonormal and the matrix D is diagonal with positive real entries. VT is the V transpose. Most Applications uses LAPACK FORTRAN implementation of SVD or it’s C/C++ equivalent code.
It is interesting to note that the LAPAC package was based on the original Fortran IV NAG library. NAG originally stood for Nottingham Algorithms Group and its history extends back into the late 1960s. It is now known as and marketed by the Numerical Algorithms Group. NAG is essentially a software library of numerical and mathematical algorithms that can be called in from user-written programs. It contains some statistical functionality, but is much more a general purpose suite.